Укажите все целые решения дробно рационального уравнения:

Ответы

vadim369 11.01.2021 13:46

$\dfrac{x^2-x}{x^2+2x+1} - \dfrac{1}{2} = \dfrac{3-x}{10x+10}\\\\\\\dfrac{x^2-x}{(x+1)^2} - \dfrac{1}{2} - \dfrac{3-x}{10(x+1)} = 0$

Теперь приводим дроби к одному знаменателю, который в данном случае будет равен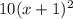 10(x+1)^2 . Для этого первую дробь мы домножаем на 10, вторую дробь - на 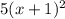5(x+1)^2 , а третью - на (x+1) . Получаем:

$\dfrac{10(x^2-x) - 5(x+1)^2 - (3-x)(x+1)}{10(x+1)^2} = 0\\\\\\\dfrac{10x^2 - 10x - 5(x^2+2x+1) - (3x + 3 -x^2 -x)}{10(x+1)^2} = 0\\\\\\\dfrac{10x^2 - 10x - 5x^2 - 10x - 5 - (2x + 3 - x^2)}{10(x+1)^2} = 0\\\\\\\dfrac{5x^2 - 20x - 5 - 2x - 3 + x^2}{10(x+1)^2} = 0\\\\\\\dfrac{6x^2 - 22x - 8}{10(x+1)^2} = 0$

Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. То есть:

$10(x+1)^2 \neq 0\\(x+1)^2 \neq 0\\x+1 \neq 0\\x \neq -1$

Приравняем числитель к нулю с учётом нашего условия:

$6x^2 - 22x - 8 = 0\ \ \ \Big| x \neq -1\\3x^2 - 11x - 4 = 0\\D = b^2 - 4ac = (-11)^2 - 4\cdot 3 \cdot (-4) = 121 + 48 = 169\\\\x_{1} = \dfrac{-b+\sqrt{D}}{2a} = \dfrac{-(-11) + 13}{2\cdot 3} = \dfrac{11+13}{6} = \dfrac{24}{6} = \boxed{\textbf{4}}\\\\\\x_{2} = \dfrac{-b-\sqrt{D}}{2a} = \dfrac{-(-11)-13}{2\cdot 3} = \dfrac{11 - 13}{6} = \dfrac{-2}{6} = \boxed{-\dfrac{1}{3}}$

Таким образом, наше уравнение имеет два решения. Но по условию нас просят отобрать только целые решения. Наш первый корень, 4, принадлежит множеству целых чисел, в то время, как второй корень,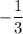 $-\dfrac{1}{3}$ , целым числом не является. Таким образом, в ответ пойдёт только $\boxed{4}$ .