Укажите уравнение, корни которого обратны корням уравнения x^2+px+q=0
Другие вопросы по теме Алгебра
Популярные вопросы
- РK1217. Кальканы немесе түссіз пленканы пайдаланып, беттестіруәдісімен...
2 - Как Булгаков воспринял революцию 1917 года?...
2 - Посещает кружки?б) В летнем латетнем лагере находились 145 детей....
1 - Запиши каждое из этих предложений в и будущем времени, используя...
1 - Решите систему уравнений методом алгебраического сложения:...
3 - ответьте на во по диалогу 1 Did Liverpool win? 2 Did Theo Walcott...
2 - Жұптық жұмыс. Сұрақтарға жауап беріп диалог кұрындар...
3 - Реши систему уравнений методом подстановки. {−z−2y+2=5z=−6−y ответ:...
1 - Найди длину, ширину, высоту параллелепипеда, котосложен из трех одинаковых...
3 - Егер шардың радиусы 10 есеге артса,шардың көлемі қалай өзрегеді...
1
Пусть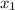 и
и  - корни уравнения
- корни уравнения 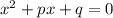 .
.
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
То есть, выполняются соотношения:
Составим новое уравнение вида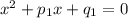 , которое имеет корни
, которое имеет корни 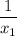 и
и  .
.
Найдем их сумму и произведение:
Получим равенства:
Уравнение имеет вид:
Или, домножив на q:
ответ: см фото.
Объяснение: