У Олега есть четыре карточки, на каждой из которых с одной и с другой стороны написаны натуральные числа (всего написано 8 чисел). Он рассматривает всевозможные четвёрки чисел, где первое число написано на первой карточке, второе — на второй, третье — на третьей, четвёртое — на четвёртой. Затем для каждой четвёрки он выписывает произведение чисел к себе в блокнот. Чему равна сумма восьми чисел на карточках, если сумма шестнадцати чисел в блокноте Олега равна 132?
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите неравенство решите неравенство: 1) х² + 5х - 6 0 2) 2х - х² ≤ 0 1)...
2 - Периметр прямоугольника равен 56 м. длина равна 20 м. чему равна ширина?...
3 - Как произносится весь текст весь 20 как произносится по к юэсей вот так the...
3 - Поезд отправился из сочи в 11 часов 20 минут (время московское) и прибыл...
2 - Read and write tom likes dancing and singing. he doesn t like painting or...
1 - Это конечно тупой вопрос но чем какают русалки ?...
1 - Замените в следующих предложениях выделенные существительные с притяжательными...
2 - Газ, объём которого в воздухе составляет 21% ?...
3 - Найти производную функции y= ln√sinx в точке x= π/4...
3 - Найдите значение в,если известно, что график функции у=-5+в проходит через...
3
18
Объяснение:
Произведение всех чисел, которые образуют все возможные четверки равно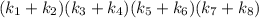 , где
, где 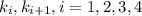 это числа записанные на i-ой карточке.
это числа записанные на i-ой карточке.
132=2*2*3*11 Так как сумма двух чисел на карточке обязательно больше 1, то есть единственный вариант представить число 132 в виде произведение 4 чисел. Поэтому искомая сумма равна 2+2+3+11=18