Алгебра: ТРИГОНОМЕТРИЯ - Упростите выражениеесли

ТРИГОНОМЕТРИЯ - Упростите выражение
если

$\sqrt{4 - 4 \sin(2 \alpha )} - \sqrt{2 + 2 \cos(2 \alpha ) }$
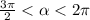
$\frac{3\pi}{2} < \alpha < 2\pi$

Ответы

ivan488 03.03.2021 04:21

1) рассмотрим сначала первый корень:

1.1 распишем синус двойного угла, вынесем 4 за скобки

1.2 единицу распишем по основному тригонометрическому тождеству как 1 = sin²a + cos²a

1.3 в скобках можно собрать формулу (а - б)² = а² + б² - 2аб

1.4 помним о том, что корень извлекается по модулю

1.5 так как по условию дано, что угол находится в 4 четверти, в которой синус отрицательный, а косинус положительный, то раскрываем модуль со знаком плюс

2) рассмотрим второй корень:

2.1 вынесем 2 за скобки и распишем косинус двойного угла

2.2 единицу распишем по основному тригонометрическому тождеству и приведем подобные слагаемые

2.3 корень извлекается по модулю, косинус раскрываем с +

3) переписываем то, что получилось, приводим подобные слагаемые