Тригонометрия будет причиной моей см*рти

Другие вопросы по теме Алгебра
Популярные вопросы
- График линейных функций y=0,5x+5...
1 - Напишите формулы следующих бинарных соединений, используя названия...
3 - С АНГЛИСКИМ тому кто все сделает...
2 - Вопросы и задания: 1. Почему в 60-х годах XIII века в Средней Азии...
1 - У девушки кругленькое лицо, как думаете?...
2 - На клетчатой бумаге с большими клетками 1см х 1см изображена фигура.Найдите...
3 - . Ниже перечислены процессы, входящие в зрительный процесс у человека....
1 - Функция задана уравнением. y=2x^2+x-3 a) В какой точке график данной...
1 - 6. Установите соответствие типы данных с названием типа....
2 - Writing Task 2. You friend is on holiday in Astana. He sent a postcard...
1
По основному тригонометрическому тождеству: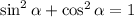 , откуда
, откуда 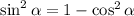 .
.
Квадрат тангенса можно выразить через квадрат косинуса по формуле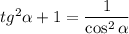 . Для нашего случая получаем:
. Для нашего случая получаем:
ответ: .
.
Объяснение: