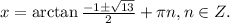Тригонометрическое уравнение : 4cos^2x-sinx*cosx-1=0 решите подробно
Другие вопросы по теме Алгебра
Популярные вопросы
- Умный надеется на свои дела, а глупый пологается на надежду , напишите...
2 - Английский 3 задания лёгкие но времени нет ...
1 - Угол AOB=44 AB=5x+4. Найти x...
3 - Проблемы Мирового океана. 3. Найдите на карте нанболее загрязненные...
2 - Масса тетрадки меньше массы книжки в 1,5 раз, среднее арифметическое...
2 - 7 класс. Проанализируйте свои знания и свой опыт реализации...
3 - Народ, а как сделать что при открытии чехла телефон включался, на...
3 - Составить программу для нахождения произведения кратных 7 находящегося...
2 - , хотя бы, которое знаете ...
3 - В треугольнике Паскаля в каждой строке сумма чисел, стоящих на чётных...
2
Если cos²x=0, то выражение написанное сверху будет представлять из себя следующее -sin²x=0, то есть sinx и cosx=0, а значит и их сумма равна 0, но по основному тригонометрическому тождеству мы знаем, что сумма квадратов косинуса и синуса всегда равняется 0 из чего можно сделать вывод, что cos²x≠0, тогда мы можем делить на него не потеряв корни.
cosx≠0 и tanx=... всегда будут пересекаться, потому что cosx≠0 это условие существования тангенса, когда cosx=0, тангенс не определён.
ответ: