Триганаметрические уровнения с одним из них, или сразу с двумя.
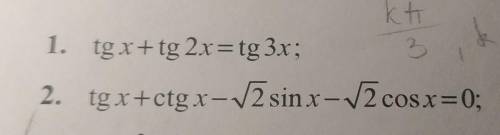
Другие вопросы по теме Алгебра
Популярные вопросы
- Сокращение добей 2•9•12/6•8•3;9•5+9•3/2•81...
1 - Задания на фото из-за большого кол-ва дз...
3 - ЗАДАНИЕ 3. Дополнения, выраженные существительными, замените дополнениями,...
1 - 1) Look at the pictures, Imagine you are on the steppe,What can you...
2 - Уравнение))135°n=180°n-360°...
1 - Чайник нагревается на кухонной плите с постоянной мощностью подачи...
1 - 6. Заполните таблицу «Восточнославянские союзы пле-мен на территории...
1 - Плоскость α проходит через вершины A и C треугольника ABC и точку...
1 - Цілі числа, починаючи з одиниці, виписані поспіль. Яка цифра буде...
1 - Төмендегі мәтінмен танысып, деңгейлік тапсырмаларды орындаңдар. 1-деңгей.Алғашқы...
1
Объединив полученные три ответа, получим окончательный ответ :