ТРИ ПРИМЕРАДАЮ ПО 5 ЗА КАЖДЫЙ
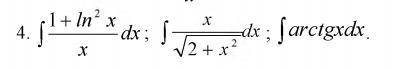
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите отзыв по рассказу Куприна ,,Тапер ответив на следующие во О чем рассказ?...
1 - В равнобедренной трапеции ABCDоснования равны 28 и 12, боковая сторона AB=20,...
2 - Заполнить таблицу источники доходов русских князей и старшей дружины 2 столбца...
1 - Самолёт летит на высоте 60 метров какое давление показывает барометр в кабине...
1 - Укажите все верные утверждения. 1. Электромагнитная волна возникает только...
1 - Зрабице вобраз Мiколки або дзеда Агея з твора Цитауки (Бел.лит.)...
1 - Вставні слова, словосполучення, речення...
1 - Визначте які проблеми були найважливішими для соціально економічного розвитку...
2 - Решите номера 4, 5 и запишите дано:...
3 - Сочинение на тему ранняя весна...
2
Объяснение:
по частям: