Требуется огородить прямоугольный участок земли так, чтобы при данном кол-ве погонных метров изгороди, равной 100 м, площадь участка была наибольшей. найдите стороны этого участка. отличники, !

догадываюсь, что макс. площадь при определённом периметре будет у квадрата.

докажем это:

обозначим стороны нашего прямоугольника как x и y

периметр его равен 2*x + 2*y = 100м

площадь S = x*y должна быть максимальной

выразим y из уравнения периметра:  y = (100 - 2*x)/2 = 50 - x

подставим вместо y в формулу площади: S = x*(50 - x)

S = -x^2+50*x

График функции S=f(x) -это парабола с ветвями, идущими вниз (т.к коэффициент при x^2 -отрицательный). Значит, максимум - это вершина параболы.

Вершина параболы лежит в точке с координатами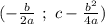

Нам нужна только координата по оси x

x = -50/(2*(-1)) = 50/2 =25м

вторая сторона участка равна:  y = 50 - 25 = 25м

ответ: это квадратный участок 25*25метров