Только 4 и 5 ⬆️⬆️⬆️⬆️⬆️⬆️⬆️
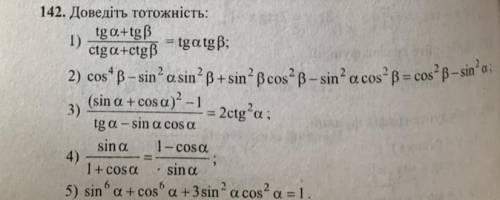
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить рассказ о произведениях пришвина.в этом тебе эти вопросы: что...
3 - 1.решить неравенство -2(g+5) больше или равно 200 2.решить неравенство...
2 - 6020: 70=? ! нужно и ещё только побыстрее и ещё примерчики 750: 50-40:...
2 - Решите. 0,48 : 6 7,9 : 316 543,4 : 143 побыстрей...
1 - Придумайте и запишите по одному предложению с плрилагательными во множественном...
2 - Собери слова в цепочку. какие слова ты соединил. почему? колыхать, покачивать,...
3 - Дайте харестиристику соболько из рассказа приёмыш...
3 - Найти сторону равнобедренного треугольника,если две из сторон 3,7 см; 7,5...
2 - Напишите сочинение про дружбу (70 слов, 9-ый класс)...
3 - Поведение человека если он попал на не обитаемый остров(робинзон крузо)...
2
Если разность левой и провой частей тождества равна нулю, то они равны . Тождество доказано .
Тождество доказано