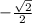Точку Р(1;0) единичной окружности повернули на угол а. Определите ее новые координаты , если известен угол а. а=-п/4. Если можно то поподробнее а то я здесь очень сильно застряла.
Другие вопросы по теме Алгебра
Популярные вопросы
- Найди в первом четверостишии синоним к слову «дети». ответ Ребята 100 процент...
3 - 3. Двуокись углерода: а) 0,5 моль; б) Подсчитайте, сколько атомов кислорода находится...
2 - 4. Сравните состав минеральной и столовой воды (по выбору). Какие вещества преобладают...
2 - Қайтымды,қайтымсыз процесттерді принціпттік айырмашылығы неде...
3 - с дз по химии 1) изомерия алканов (не менее 20примеров) и реакции на примере бутана;...
3 - 1.Пользуясь масштабам физической карте полушарий в атласе для пятого класса, определите...
3 - Балет Жизель написать конфликт пьесы и действующих лиц...
2 - на сканере за первую часть отсканировали 2/ 5 произведения за за второй час 1/3...
3 - Обьем воды и тела если всего 100мл а без камня 55?...
1 - До ть будь ласка. Дуже сильно потрібно. Часу самій робити не вистачає. Переклад....
3
Единичная окружность - окружность с центром в точке О(0;0) и радиуса R=1 .
Абсциссы точек, находящихся на единичной окружности равны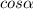 , а ординаты -
, а ординаты - 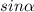 , где угол
, где угол 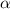 - угол между осью ОХ и радиус-вектором точки Р (отрезком ОР), лежащей на ед. окружности . Можно записать координаты точки Р в виде
- угол между осью ОХ и радиус-вектором точки Р (отрезком ОР), лежащей на ед. окружности . Можно записать координаты точки Р в виде 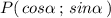 .
.
Точка Р(1;0) находится на пересечении оси ОХ и ед. окружности .
Если повернуть точку Р на угол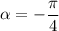 , то она повернётся в отрицательном направлении , по часовой стрелке, на угол в
, то она повернётся в отрицательном направлении , по часовой стрелке, на угол в 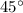 и займёт своё положение на пересечении биссектрисы 2 и 3 координатных углов и окружности . Получим точку
и займёт своё положение на пересечении биссектрисы 2 и 3 координатных углов и окружности . Получим точку 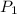 .
.
Поэтому координаты точки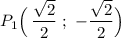 .
.
ответ:-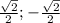
Объяснение:
Координата x это cos, а y это sin, следовательно(по таблице значений синуса и косинуса),cos(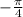 ) =
) = 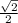 , sin(
, sin(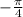 ) =
) =