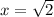![\sqrt[x]{81} = 3 {}^{2x}](/tex.php?f= \sqrt[x]{81} = 3 {}^{2x} )
и

надо найти x-?
Другие вопросы по теме Алгебра
Популярные вопросы
- Отметьте части клетки на рисунке выполняющие следующие функции назовите...
3 - Игральную кость бросают дважды. найдите вероятность того, что в...
2 - Ракета массой 357 кг стартовала с начальной скоростью 22 м/с. определи...
3 - Напишите текст правильно, язык. . мне ; *( надо поставить пробелы...
3 - Сократить два последних абзаца ❤️ ( 73 )...
1 - Вычислите кинетическую энергию вороны массой 900г летящей со скоростью...
3 - Выберите все характеристики протонаучного знания 1) имеет сакральный...
3 - Где находится йеллоустоунскийпарк...
3 - Під час змагань з бігу перший учень пробіг 10 хв зі швидкістю 12...
1 - Решите вариант,который слева на доске...
2
Однако в показателе степени корня может стоять лишь натуральное число, большее 2. А значит данное уравнение корней не имеет.
_________________________________
Если же в исходном условии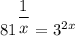 , то рассматриваем далее неравенство, подставляя в него полученные значения:
, то рассматриваем далее неравенство, подставляя в него полученные значения:
Заметим: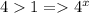 возрастает.
возрастает.
Тогда