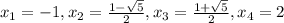решить показательное уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишіть оповідання бездумний вчинок за поданим сюжетом складіть обрамлення...
3 - Найти массу оксида серы (vi) который получиться при окислении 500 кг...
1 - №506 указать грамматические основы указать обстоятельство и деепричастия...
3 - Как вы понимаете слова тургенева ,,у щастья есть только настоящее - и...
3 - Спишите .укажите лицо видилите прилагательние в тексте мой дркг...
1 - Обчисліть масу тристеаринового жиру, що необхідно піддати омиленню для...
3 - Скласти речення з різними зв язку щоб у ньому були слова зі свого боку...
2 - Найдите площадь фигуры ограниченной линиями y=2х y=0 x=1 и x=3...
2 - Переведите, на казахский! берегите глаза. глазами мы видим мир и красоту....
2 - Решите по действиям на листочках ...
1
a^-n = 1/a^n
a^m * a^n = a^(m+n)
3^(x^2 - x) + 3^(3 + x - x^2) = 12
3^(x^2 - x) + 3^3*3^(x - x^2) = 12
3^(x^2 - x) + 27/3^(x^2 - x) = 12
3^(x^2 - x) = t > 0
t + 27/t - 12 = 0
t^2 - 12t + 27 = 0
D = 12^2 - 4*27 = 144 - 108 = 36
t12 = (12 +- 6)/2 = 3 9
t1 = 3
3^(x^2 - x) = 3
x^2 - x = 1
x^2 - x - 1 = 0
D = 1 + 4 = 5
x12 = (1 +- √5)/2
t2= 9
3^(x^2 - x) = 3^2
x^2 - x = 2
x^2 - x - 2 = 0
D = 1 + 8 = 9
x34 = (1 +- 3)/2 = -1 2
ответ -1, 2, (1 + √5)/2, (1 - √5)/2
Объяснение:
ответ: