теорема Виета x1+x2=6
x1x2=-8
x1=?
x2=?
пример:
x2+4x-5=0
x1+x2=-4
x1x2=-5
x1=-5
x2=1

Ответы

AMK525 11.04.2022 06:20

Тк корни иррациональные будут, по Виета тут врят ли решить можно, попробуй через дискриминант

теорема Виета x1+x2=6x1*x2=-8x1=?x2=?пример:x2+4x-5=0x1+x2=-4x1*x2=-5x1=-5x2=1

ПОКАЗАТЬ ОТВЕТЫ

embazuka 11.04.2022 06:20

Объяснение:

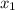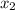Если x_1 и x_2 - корни квадратного уравнения 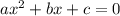ax^2+bx+c=0 , то сумма корней равна отношению коэффициентов 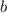и , взятому с противоположным знаком, а произведение корней равно отношению коэффициентов и .

$ax^2+bx+c=0left \{ {{x_1+x_2=-\frac{b}{a}} \atop {x_1+x_2=\frac{c}{a}}} \right. \\$

Наиболее часто теорема Виета используется применительно к приведенному квадратному уравнению вида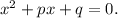 x^2+px+q=0.

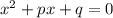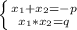Сумма корней приведенного квадратного уравнения x^2+px+q=0 равна коэффициенту при , взятому с противоположным знаком, а произведение корней - свободному члену, то есть, $\left \{ {{x_1+x_2=-p} \atop {x_1*x_2=q}} \right.$ .

$x^2-6x+8=0left \{ {{x_1+x_2=6} \atop {x_1*x_2=-8}} \right. \left \{ {{x_1=2} \atop {x_2=4}} \right. x^2+4x-5=0left \{ {{x_1+x_2=-4} \atop {x_1*x_2=-5}} \right. \left \{ {{x_1=-5} \atop {x_2=1}} \right.$