Теорема 1. Сумма внутренних углов многоугольника равна 180° ( п -2). Доказательство:

Отмечу во внутренней области п -угольника произвольной точки вывода .

Соединим точку O с каждой вершиной n -угольника, при этом получим n треугольников.

Сумма углов одного треугольника равна 180° .

Тогда сумма внутренних углов многоугольника равна сумме всех углов этих треугольников за вычетом центрального угла при точке O , который равен360° .

Итак, треугольников у нас n , поэтому сумма углов всех треугольников равна n ∙180° , вычитаем отсюда центральный угол, то есть360° , получим n ∙180° -360° = 180° ∙ ( п -2) - формула суммы внутренних углов многоугольника.



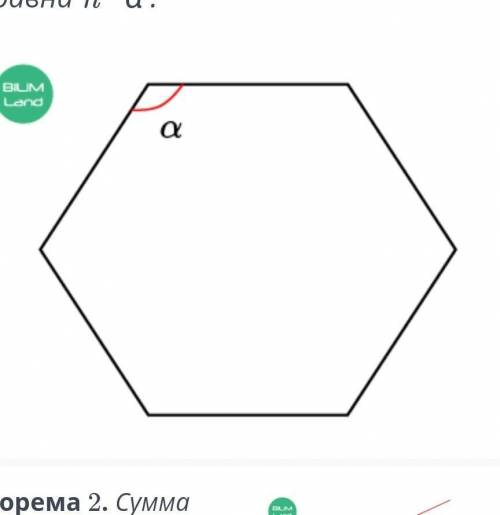
Следствие.Сумма внутренних углов правильного многоугольника с вершиной α равна n ∙ α .



Теорема 2. Сумма внешних углов выпуклогоугольника, взятых по одному при каждой вершине равна 360° .

Доказательство:

Внешний угол соответствующий с соответствующим внутренним углом, поэтому их сумма равна 180° . Тогда, чтобы найти сумму всех внешних углов многоугольника, нужно180° умножить на n и вычесть сумму внутренних углов многоугольника.

180° ∙ п -180° ( п -2) = 360°

Итак, сумма внешних углов любого выпуклого многоугольника взятых по одному при каждой вершине, равна 360° .

​50б

кадитагаев    1   08.09.2020 11:15    4