Тема урока: Квадратичные функции вида y=a(x-m)², y=ax²+n и y=a(x-m)²+n при a≠0, их графики и свойства , варианты ответа на фото.

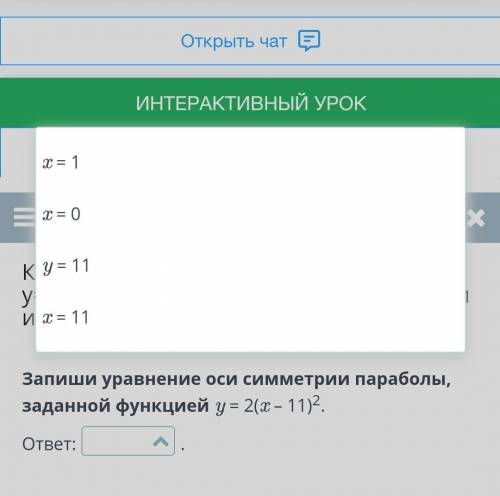
уравнение оси симметрии параболы х=11

Объяснение:

у=2(х–11)²

раскроем скобки по формуле сокращённого умножения:

(а–b)²=a²–2ab+b²:

(х–11)²=х²–22х+121 при этом мы можем не умножать число 2 на это выражение и найти уравнение оси симметрии параболы.

В трёхчлене х²–22х+121, а=1, b= –22, c=121; ось симметрии вычисляется по формуле:

х=11 – это искомое уравнение оси симметрии параболы

Можно для эксперимента трёхчлен умножить на 2:

2(х²–22х+121)=2х²–44х+242, тогда:

х=11.

Получается одно и то же, поэтому первого варианта будет достаточно