Алгебра: там три задания, сложные и они в приложении пли:з

там три задания, сложные и они в приложении
пли:з

Ответы

darasnezko297 14.10.2020 12:30

1) D(y)=(-∞; ∞), Е(у)= (-∞; 5]

2) D(y)= (-∞; 0)∪(0;+∞). график в приложении (первый график в виде параболы с ветвями вверх)

3) график тоже в приложении (второй график - в виде ломанной)

Объяснение:

1) Так как это полином, то нет особых точек функции, где она бы не существовала, значит эта функция определена на всей оси ОХ.

D(y)=(-∞; ∞).

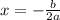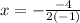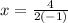Область значений найти несколько сложнее. Так как это парабола с ветвями, направленными вниз, то надо найти координаты вершины параболы. Координата вершины параболы ищется по формуле: $x=-\frac{b}{2a}$ . Подставим известные данные: $x=-\frac{-4}{2(-1)}$ . Или $x=\frac{4}{2(-1)}$ , х=-2.

Тогда у(-2)=-(-2)²-4(-2)+1. у(-2)=-4+8+1. у(-2)=5. Так как это парабола с ветвями, направленными вниз, то все ее остальные значения будут меньше 5. Значит область значений меняется от (-∞) до 5 включительно.

Е(у)= (-∞; 5]. Третий график в приложении. Он подписан.

2) Если сократить числитель и знаменатель на х, то получим функцию f(x)=x²-6x+5 - обычная парабола с вершиной в точке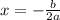 $x=-\frac{b}{2a}$ , то есть 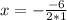$x=-\frac{-6}{2*1}$ или х=3. При этом у=3²-6*3+5, то есть у=9-18+5. Или у=-4.

Вершина параболы в точке (3; -4). Точки пересечения с осью оХ можно найти, если функцию приравнять к нулю. То есть x²-6x+5=0. Нетрудно увидеть, что

(х-1)*(х-5)=0.

х₁=1, х₂=5 - в этих точках парабола пересекает ось ОХ. Ветви параболы направлены вверх, так как коэффициент при старшем члене равен 1>0.

В точке х=0 функция у(х) не существует, так как х, находясь в знаменателе, позволяет взять предел данной функции. Предел этой функции в точке х=0 равен значению f (x). То есть f (0)=(0-1)*(0-5),

f(0)=5. Это место на графике можно указать стрелками.

Область определения этой функции будет (-∞; 0)∪(0;+∞).

То есть D(y)= (-∞; 0)∪(0;+∞). График функции смотрите в приложении.

$y=\frac{x^3-6x^2+5x}{x}$