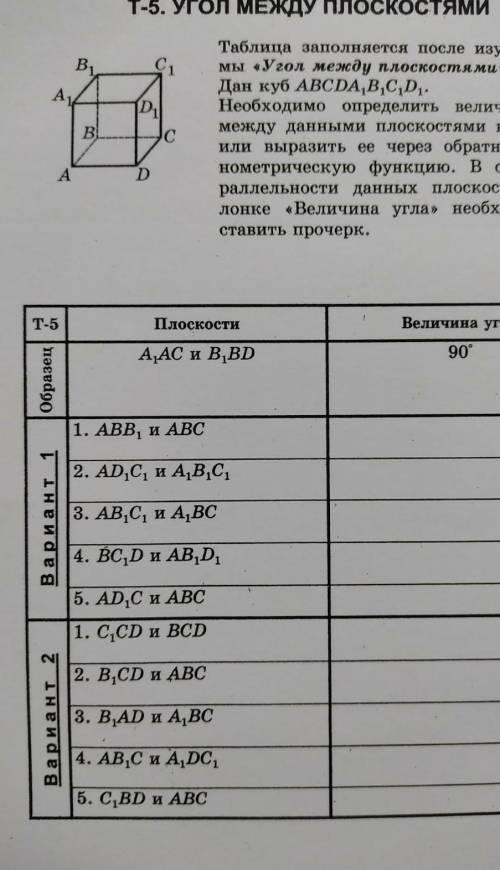
Т-5. УГОЛ МЕЖДУ ПЛОСКОСТЯМИ Таблица заполняется после изучения те мы Угол между плоскостями». B1 A₁ D₁ B JC A Дан куб ABCDA,B,C,D.. Необходимо определить величину угла между данными плоскостями в градусах или выразить ее через обратную триго нометрическую функцию. В случае па раллельности данных плоскостей в ко лонке Величина угла необходимо по ставить прочерк.
Другие вопросы по теме Алгебра
Популярные вопросы
- Определить стиль,жанр и тд.все на фото...
2 - Ex. 1 Answer the questions: 1.What is the capital of Great Britain? 2.How many...
2 - Реакция протекающая между оксидом железа 3 и алюминием относится к реакциям 1)разложения...
2 - Белка и бурундук запасали орехи на зиму, Бурундук нашел запасы белки и утащил...
2 - 2sin²45°-4cos³60° 6ctg²60°-2sin²30° ...
2 - 4. Спиши. Вставь пропущенные буквы. Объсни их написание.Используя опорные слова,...
3 - Твір на тему , моя подорож до савани...
3 - На прямой отмечены точки , , , , (необязательно в таком порядке) так, что расстояния...
2 - 4 4166. Найдите сумму.4 2а)+ 1;+б б) 4 +3+ в) 1 * 2 *+112г) 12 +ою+167. Найдите...
2 - характеристика Александра II по плану: 1)годы рождения и правления 2)краткий план...
1
Шаг 1: Найдем угол между сторонами.
Нам дан куб ABCDA₁B₁C₁D₁, где A, B, C, D - вершины куба, а A₁, B₁, C₁, D₁ - середины сторон соответствующих ребер.
Для нахождения угла между сторонами, построим треугольник ABC.
Шаг 2: Найдем угол BAC (α).
Заметим, что треугольник ABC - прямоугольный, так как AB, BC и AC являются сторонами куба. Угол BAC (α) - прямой угол (90 градусов), так как это угол основания куба.
Шаг 3: Найдем угол между пространственными диагоналями.
Для этого построим два отрезка: один соединяющий точки A₁ и C₁, а другой - точки B и D₁.
Шаг 4: Найдем угол между пространственными диагоналями (β).
Для нахождения угла между пространственными диагоналями, будем использовать тригонометрические функции. Рассмотрим треугольник A₁C₁D₁:
- Найдем длины сторон треугольника AC₁ и A₁D₁, используя теорему Пифагора.
AC₁ = √(AB₁² + BC₁²)
AC₁ = √(1² + 1²)
AC₁ = √2
A₁D₁ = √(AB₁² + AD₁²)
A₁D₁ = √(1² + 1²)
A₁D₁ = √2
- Найдем косинус угла C₁A₁D₁ (β) по формуле:
cos β = (AC₁² + A₁D₁² - C₁A₁²) / (2 * AC₁ * A₁D₁)
cos β = (2 + 2 - 1) / (2 * √2 * √2)
cos β = 3 / 4
cos β = 0.75
Шаг 5: Найдем величину угла между пространственными диагоналями.
Для этого воспользуемся обратной тригонометрической функцией арккосинуса.
β = arccos(0.75)
β ≈ 41.41 градусов
Итак, величина угла между данными плоскостями равна примерно 41.41 градусов.