Существует бесконечно множество квадратов выражения форм 50^m- 50^n, но не одного квадрата выражения 2020^m+2020^n;
при этом m и n позитивные числа.
докажите, что это правда.

Question

Алгебра: Существует бесконечно множество квадратов выражения форм 50^m- 50^n, но не одного квадрата выражения 2020^m+2020^n; при этом m и n позитивные числа. докажите, что это правда.

Cfhbcbudh · Answer

1) Существует бесконечно много квадратов натуральных чисел, представимых в виде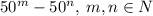 $50^m- 50^n,\: m,n\in N$ .

Для доказательства этого факта достаточно взять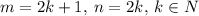 $m=2k+1,\: n=2k, \: k\in N$ . И правда: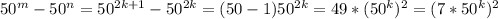 $50^m- 50^n=50^{2k+1}-50^{2k}=(50-1)50^{2k}=49*(50^k)^2=(7*50^k)^2$

2) Не существует квадратов натуральных чисел, представимых в виде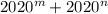 2020^m+2020^n .

Для этого рассмотрим остаток от деления выражения на 3: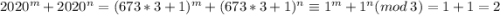 $2020^m+2020^n=(673*3+1)^m+(673*3+1)^n\equiv 1^m+1^n(mod\:3)=1+1=2$

С другой стороны, квадрат натурального числа может давать остатки 1 или 0 при делении на 3. И правда: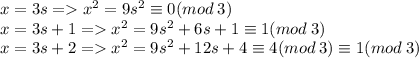 $x=3s=x^2=9s^2\equiv0(mod\:3)\\ x=3s+1=x^2=9s^2+6s+1\equiv1(mod\:3)\\ x=3s+2=x^2=9s^2+12s+4\equiv4(mod\:3)\equiv1(mod\:3)$