Сумма всех целых значений выражения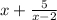
при целочисленных x равна

16

Объяснение:

Т.к. предполагается целочисленное значение выражения, то при целочисленном х значение дроби

тоже должно быть целым.

Т.к. 5 - число простое, то оно делится лишь на 1 и на самое себя:

Т.е. целочисленные значения выражение принимает только при х = 3 или х = 7

При x = 3 :

При х = 7:

Сумма выражений составит:

8 + 8 = 16

ответ: 16