1. Алгебра
  2. Сумма первого и пятого членов

Сумма первого и пятого членов геометрической прогрессии равна 51, а сумма второго и шестого членов прогрессии равна 102. Найдите знаменатель и первый член данной прогрессии.

KristinaPech KristinaPech    3   25.12.2020 20:41    4

Ответы
SofiCoRainbow1 SofiCoRainbow1  12.02.2021 21:14

b_{2} = b_{1}q\\\\b_{5} = b_{1}q^4\\\\b_{6} = b_{1}q^5

Нам известно, что сумма первого и пятого членов геометрической прогрессии равна 51, а сумма второго и шестого членов равна 102.

\begin{equation*}\begin{cases}b_{1} + b_{5} = 51\\b_{2} + b_{6} = 102\end{cases}\end{equation*}

Разделим верхнее уравнение на нижнее:

\dfrac{b_{1}+b_{5}}{b_{2} + b_{6}} = \dfrac{51}{102}\\\\\\\dfrac{b_{1} + b_{1}q^4}{b_{1}q + b_{1}q^5} = \dfrac{1}{2}

По основному свойству пропорции:

2\left(b_{1} + b_{1}q^4\right) = b_{1}q + b_{1}q^5\\\\2b_{1} + 2b_{1}q^4 = b_{1}q\left(1 + q^4\right)\\\\2b_{1}\left(1 + q^4\right) = b_{1}q\left(1+q^4\right)\ \ \ \ \ \Big| : b_{1}\left(1+q^4\right)\\\\\boxed{\bf{q = 2}}

Мы нашли знаменатель. Найти первый член мы можем, например, из нашего первого уравнения.

b_{1} + b_{5} = 51\\\\b_{1} + b_{1}q^4 = 51\\\\b_{1}\left(1 + q^4\right) = 51\\\\b_{1}\left(1 + 2^4\right) = 51\\\\b_{1}(1 + 16) = 51\\\\17b_{1} = 51\ \ \ \ \ \Big| :17\\\\\boxed{\bf{b_{1} = 3}}

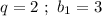ответ: q = 2\ ;\ b_{1} = 3.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
alenashafeeva alenashafeeva  20.10.2020 15:59
впиши в пустые клетки знаки плюс или минус так чтобы полученное равенство было тождеством1)х (+-) 9 (+-) х (+-) 7=22)m (+-) n (+-) 2m (+-) 4n (+-) 3m (+-) 8n=3n3)4y (+-)...
florzy florzy  20.10.2020 16:00
При каком значении переменной разность выражений 4а+8 на 3 больше значения выражения 3-2a...
Mira12202 Mira12202  20.10.2020 16:00
Может ли радиус описанной около треугольника окружности быть: 1) больше каждой стороны; 2) меньше каждой стороны; 3) равнымкаждой стороне этого треугольника?​...
JoYCasinI2558 JoYCasinI2558  20.10.2020 15:17
Какие из чисел 3 - 2 и 1 являются корнями уравнения x + 3 равно 6 5 x - 8 равно 2 x плюс 4?​...
КоТэПрЕзИдЕнТэ КоТэПрЕзИдЕнТэ  20.10.2020 15:15
Чай расфасовали в 30 пачек, 150 г в каждой. сколько пачек получится, если это же количество чая фасовать в пачке по 250?​...
kfkkffkdkd kfkkffkdkd  20.10.2020 15:15
Какова вероятность того, что герб упадет более 5 раз, если монету подбросить 7 раз?​...
екатерина698 екатерина698  20.10.2020 15:15
На 6 одинаковых костюмов потребовалось 22 м ткани. сколько ткани нужно для пошива 15 таких же костюмов. ​...
Roflobara Roflobara  20.10.2020 15:15
Как разрезать произвольную трапецию на 9 равнобедренных треугольников?...
Dariu111 Dariu111  20.10.2020 15:15
Докажи, что четырёхугольник ABCD является прямоугольником, найди его площадь, если A(14;2), B(23;8), C(17;17) и D(8;11)....
katrinzeta18 katrinzeta18  10.12.2021 04:49
Вынеси общий множитель за скобки: !!...

Популярные вопросы