Сумма квадратов цифр некоторого двухзначного числа равна 26. произведение данного числа на число, записанное теми же цифрами,но в обратном порядке, равно 765. найдите это число. желательно с решением
Другие вопросы по теме Алгебра
Популярные вопросы
- Твір на тему людина починається з добра...
3 - При сушке яблок теряют 3\4 своей массы. сколько получится сухофруктов...
3 - 1. объем выделившегося кислорода при регенерации пероксидом натрия...
2 - Выпишите цифры( прсьба пояснить), обозначающие запятые между частями...
2 - Какой объем угарного газа необходимо сжечь для получения 1000кдж теплоты,если...
2 - Найти угловой коэффициент касательной проведенной в точку с ординатой...
2 - 1.прирастворении в соляной кислоте 25,8 г сплава выделилось 2,24 л...
2 - Аллегория,олицетворение,мораль в басне.дайте определение понятий!...
2 - За месяц магазином было продано 360 сотовых телефонов. 234 из них были...
3 - На автостоянке стояло 10 машин и велосипедов двухколесных.всего было...
2
Пусть х-цифра десятков, а у - цифра единиц некоторого двузначного числа. Тогда само число 10х+у, а число записанное теми же цифрами в обратном порядке 10у+х. (10х+у)*(10у+х)-произведение чисел, - сумма квадратов цифр. По условию произведение равно 765, а сумма квадратов цифр 26. Получим систему уравнений:
- сумма квадратов цифр. По условию произведение равно 765, а сумма квадратов цифр 26. Получим систему уравнений:
Получим или
или 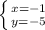 или
или  или
или 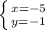
Так как х и у - цифры, то x>=0 и y>=0. Значит, или
или 
Итак, данное число либо 15, либо 51.
ответ: 15 или 51.