Сумма квадратов цифр двузначного числа равна 50. если из этого числа вычесть 54, то получится число,записанное теми же цифрами,но в обратном порядке . найдите данное число

Пусть первая цифра двухзначного числа - а, а вторая - в. Тогда по условию можно составить два уравнения, которые образуют систему: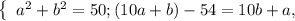

 Преобразовавший второе уравнение, получим: 9а-9в=54 (54/9=6) или а-в=6. Отсюда а=в+6. Подставим в первое вместо а=в+6 и после его преобразования получим квадратное уравнение2b^2+12b-14=50 или 
b^2+6b-7=0. Корнями его будут 1 и -7. Так как речь идет о натуральных числах, то отрицательный корень будет лишний. Подставив в=1 в а=в+6=1+6=7. 
ответ: 71 и 17.

Пусть x - количество десятков и y - количество единиц; тогда 10x+y - данное число. Используя данные задачи, составляем систему уравнений: 

x2+y2 = 50; 10x+y-54 = 10y+x 

x2+y2 = 50; 10x+y-54 -10y-x = 0

x2+y2 = 50; 9x-9y-54 = 0

x2+y2 = 50; 9(x-y-6) = 0

x2+y2 = 50; x-y-6 = 0

x2+y2 = 50; x = y+6

(y+6)2+y2 = 50; y2+12y+36+y2 = 50; 2y2+12y+36 = 50; 2y2+12y+36-50 = 0; 2y2+12y-14 = 0; 2(y2+6y-7) = 0; y2+6y-7 = 0; (y+7) (y-1) = 0; y+7 = 0 v y-1 = 0; y = -7 v y =1; но по смыслу задачи y>0; поэтому y не равен -7; y = 1; x = 1+6 = 7; данное число - 71.

ответ: 71.