сумма чисел x y z равно 25.Числа x 2y z являются частью арифметической прогрессии, числа x y+1 z евлются частью геометрической прогрессии, найдите числа ответьте быстрее
Другие вопросы по теме Алгебра
Популярные вопросы
- (решите который посередине) 6 класс. Математика....
3 - Не розвязуючи рівняння знайдіть суму і добуток його коренів,Встановіть відповідність....
2 - 3 Complete the short dialogues. Dialogue 1A: Do you fancy (1)to the cinema...
3 - Вес груза подвешенного к концу веревки составляет 400 Н. Какую силу надо...
1 - 1. Назовите основную причину падения республики в Риме. 2. Как произошло...
2 - Образуйте от сильных и слабых глаголов формы Partizip II (причастие 2) и...
2 - Мен ... жакшы көрөм. Мен ... кызыгам, анткени ...Менин үй-бүлөм ... жакшы...
2 - 1))В геометрической прогрессии b4:b2=9 b4=108 Найдите b3...
1 - БРОО ))) Мораль байки Л. Глібова «Жаба і Віл» - це … Виберіть одну відповідь:...
2 - Также где то или Так же где то?...
3
Используем два факта:
1) Если три последовательных числа являются членом арифметической прогрессии, то среднее является средним арифметическим:
2) То же самое с геометрической прогрессией — там средним геометрическим:
Поработаем со вторым уравнением, используя первое:
Первое уравнение нам больше не нужно. Упростим уравнения (2) и (3):
Используем обратную теорему Виета, где второй член равен сумме корней, взятой со знаком минус, а третий член — произведению:
Я сразу по теореме Виета вижу корни: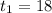 ,
, 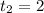 . Можете решить через дискриминант.
. Можете решить через дискриминант.
В итоге получили, что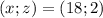 либо
либо 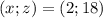 (ещё из условия было видно, что обе прогрессии симметричны относительно убывания/возрастания).
(ещё из условия было видно, что обе прогрессии симметричны относительно убывания/возрастания).
ответ: 18, 5, 2 либо 2, 5, 18.