Сторона правыльного трикутника вписаного в коло доривнюе 4корней из 6 см знайдить сторону квадрата вписаного у це коло
Другие вопросы по теме Алгебра
Популярные вопросы
- Подготовить подробный ответ на вопрос: какие картины рисует автор, рассказывая...
1 - __ подписание великой ремонстрации __ начало работы долгого парламента __ подписание...
1 - Срешением, у трикутнику abc відрізок bk-висота,відрізок ам-бісектриса,md=6см...
1 - Укажіть послідовність нуклеотидів в обох ланцюгах фрагмента днк якщо відомо...
3 - Примеры , когда сила трения вредна ( не менее 10 ). ответ обоснуйте...
2 - Подробно письмо много ответ на письмо 80-100слов...
1 - Сочинить сказку на тему новогоднее чудо с героями славянских мифов....
1 - Найди значение выражения: 34⋅1,1⋅1155: 15= (первое окошко — результат числителя,...
1 - Решите уравнения: a)3x²-12=0 б)2х²+6х=0 в)9у²-4=0 г)8у²+у=0 д)(х+1)(х-2)=0 е)(х-0,5)(х+1/7)(х+2,1)=0...
2 - [tex]\sqrt[7]{\frac{81^{4} }{9} }[/tex]...
3
Находим радиус описанной около треугольника окружности:
Диагональ квадрата равна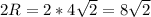 (см)
(см)
Сторона квадрата вписанного в окружность равна(по теореме Пифагора)
ответ: 8 см
формула Радиуса описанной окружности вокруг правильного треугольника равна. R=a·√3/3 R=4√6·√3/3=4√18/3=12√2/3=4√2-радиус окружности,диагональ квадрата =диаметру окружности=4√2·2=8√2 Пусть х-сторона квадрата,тогда по теореме Пифагора х²+х²=(8√2)² 2х²=128 х²=64 х=8 см-сторона квадрата