1. Алгебра
  2. Срешением : [tex] \sqrt{2x -

Срешением : \sqrt{2x - 3} + \sqrt{4x + 1} = 4​

lakomka2018 lakomka2018    3   19.04.2019 00:06    1

Ответы
IlyaLzt IlyaLzt  08.06.2020 00:10

2

Объяснение:

1-й Угадываем x=2 (проверка: 4=4). Поскольку левая часть возрастает, а правая постоянна, других решений нет.

2-й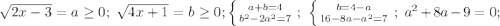 \sqrt{2x-3}=a\ge 0;\ \sqrt{4x+1}=b\ge 0; \left \{ {{a+b=4} \atop {b^2-2a^2=7}} \right. ;\ \left \{ {{b=4-a} \atop {16-8a-a^2=7}} \right. ;\ a^2+8a-9=0;

(a+9)(a-1)=0;\ \left [ {{a=-9} \atop {a=1}} \right.;\ a\ge 0\Rightarrow a=1; 2x-3=1^2; x=2.

Проверка: 1+3=4 - верно.

3-й Стандартный с двойным возведением в квадрат самый муторный. Надеюсь, что автор второго решения приведет именно его. А меня увольте.

4-й Угадываем x=2: 1+3=4. Преобразуем уравнение к виду

(\sqrt{2x-3}-1)+(\sqrt{4x+1}-3})=0.

Каждую скобку домножим и разделим на сопряженную к ней (очевидно, что сопряженные выражения не равны нулю):

\frac{(\sqrt{2x-3}-1)(\sqrt{2x-3}+1)}{\sqrt{2x-3}+1}+\frac{(\sqrt{4x+1}-3)(\sqrt{4x+1}+3)}{\sqrt{4x+1}+3}=0;\ \frac{2(x-2)}{\sqrt{2x-3}+1}+\frac{4(x-2)}{\sqrt{4x+1}+3}=0.

Поскольку x=2 мы уже угадали, можем теперь считать, что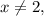 x\not= 2, и сократить на (x-2). Получим

\frac{2}{\sqrt{2x-3}+1}+\frac{4}{\sqrt{4x+1}+3}=0.

Поскольку левая часть положительна, а правая равна нулю, это уравнение решений не имеет.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
аслансосланов аслансосланов  15.08.2019 16:00
Выполните возведение одночлена в степень: а)(4ху)^2= б)(2а^2c^3)^3= 1/2mn)^3= )^4= )3= )^4=...
dora12345pandora dora12345pandora  19.05.2020 18:17
Розкласти на множники квадратний тричлен 1) 2х^2-8х-10 2) -х^2+3х...
ama14 ama14  19.05.2020 18:17
Чи проходить графік функції y=2x-5 через точку A((-1;-7)​...
Trolololo09 Trolololo09  19.05.2020 18:17
Решите графически систему уравнений х-у=5, х+2у=-1Задание смотрите в скриншоте оформите правильно!! ​...
Mashyanova2016 Mashyanova2016  19.05.2020 18:17
Дано: sina = 0,6, sing = -0,28, 0 a 5, п B Вычислите: 1) cos(а - в); 2) sin(a+B); 3) cos(а+в).​...
GGGKazakhstan GGGKazakhstan  19.05.2020 18:17
Якому одночлену дорівнює вираз 3ab∧4×(-2a²b³)​...
vipkakunina vipkakunina  17.04.2020 08:32
9у/у-b к дроби со знаменателем b-y...
Scared911 Scared911  17.04.2020 08:31
1)(x-3)(3x^2-4x-20)/7x^2-27x-40≥02)1/x-3≥x-2​...
Angelaby Angelaby  17.04.2020 08:31
Не решая уравнение x2+4x+7x+28=0 , определи, имеет ли оно корни....
Comicsans123 Comicsans123  17.04.2020 08:31
Дано линейное уравнение с двумя переменными5x−9y+30=0.Используя его, запиши переменную y через другую переменную x.​...

Популярные вопросы