Сравните значения выражения: √27 и 4√3 3√2 и 2√3 вынесите множетель из под знака корня: а) √у(в кубе) в)√7у(в 8-ой степени) с ришением.=)
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинить сказку о чём шепчутбся раки...
1 - Биография о ветеранах великой отечественной войны...
1 - Почему не удался первый побег ? автор л.н.толсой кавказский пленник...
2 - Водяная капля разделилась одна с зарядом +3 g а вторая с зарядом -2q каким...
1 - Морфологические критерии паслена черного...
1 - Кто правильно напишет 40 ! умоляю пишите ответ ! дан правильный шестиугольник...
2 - Для наполнения бассейна используются две трубы.через первую трубу за 1 мин...
2 - Система линейных уравнений. 4z-5y=1 5y-4z=3...
2 - Сочинение рассуждение на тему умеем ли мы сострадать?...
1 - Решите уравнение а)15x=0,15б)3,08: y=4е)8р-2р-14,21=75,19...
2
1)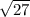 и
и 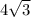 ,
,
2)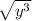 =
= 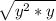 =
= 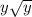
1. √27=√9•3=√3²•3
Выносим 3 за корень. Получаем 3√3
Сравниваем выражения:
3√3<4√3
2.В первом выражении вносим 3 под корень:
√3²•2=√9•2=√18
Во втором выражении вносим 2 под корень:
√2²•3=√4•3=√12
Сравниваем выражения:
√18>√12
3.√y^3(в степени 3)=√y²•y=y√y
4.√7y^8=√7•(y^4)²
Выносим у в степени 4 из-под корня:
у^4√7