Спростити вирази 1
2.
Очень нужно
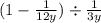
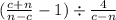
Другие вопросы по теме Алгебра
Популярные вопросы
- Число которое находится между числами 63 и 65 уменьшить на 7...
1 - Знайдіть похідну f(x)=x^2+x^-3...
3 - Какие обязоности у шаньюя?...
3 - Як розподіляються живі організми на Землі???...
2 - В равнобедренном треугольнике KMC на высоте CH, проведённой к...
2 - В каком предложении нет союза? (знаки препинания не расставлены!)...
2 - Что произойдёт в колебательном контуре при отсутствии внешней...
3 - Якщо х=2 то у=?якщо X = -2 то ігрик = скільки ...
2 - Собачье сердце 6 глава за диалогом Швондера и профессора Преображенского,...
1 - укр мова кто знает напишите ответ...
3
Объяснение:
1 .
2.
Поскольку
то