Сподробным решением, ! 1) найти значение выражения 3sqrt2*2^(1/2)- корень из 16 в степени 4 2)вычислить 8^(2-log числа 6 по основанию2) +5^(-log числа27 по основанию 5) 3) найти сумму корней уравнения 9^ (x-1/2)=27^(x^2-1)

Ответы

Infasotka41 17.06.2020 23:59

1) Если я правильно понял автора, вижу так:

$3\sqrt2*2^{\frac{1}{2}}-\sqrt{16^4}=3\sqrt2*\sqrt2-16^2=3*2-256=-250$

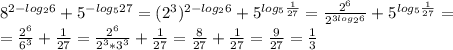
2) $8^{2-log_26}+5^{-log_527}=(2^3)^{2-log_26}+5^{log_5\frac{1}{27}}=\frac{2^6}{2^{3log_26}}+5^{log_5\frac{1}{27}}= \\\ =\frac{2^6}{6^3}+\frac{1}{27}=\frac{2^6}{2^3*3^3}+\frac{1}{27}=\frac{8}{27}+\frac{1}{27}=\frac{9}{27}=\frac{1}{3}$

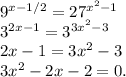
3) $9^{x-1/2}=27^{x^2-1} \\\ 3^{2x-1}=3^{3x^2-3} \\\ 2x-1=3x^2-3 \\\ 3x^2-2x-2=0.$

D=(-2)²+24=28>0. Значит, уравнение имеет 2 корня х₁ и х₂.

Получили, что исходное показательное уравнение равносильно квадратному. Значит, согласно теореме Виета

$x_1+x_2=-\frac{b}{a}=\frac{2}{3}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

ALLAHJIJA 02.07.2019 00:00

Решить! нужно.есть перевод на . 83 ! на одному скаладі вугілля на 800 т більше, ніж на другому. після того як з першого складу забрали 60% вугілля,а з другого 50...

Kettiplay 02.07.2019 00:00

Смешали некоторое количество 17 процентного раствора некоторого вещества с таким же количеством 81 процентного раствора этого же вещества. сколько процентов составляет...

cherenko85 02.07.2019 00:00

(нужно ) найдите область допустимых значений выражения : arcsin(2-8x); arccos(4-x ). 3...

mariaalimardonova 01.07.2019 22:16

Решите уравнение. чтобы посмотреть уравнение нажмите на картинку...

stolyarovsemen 01.07.2019 22:12

Решить выражение: ((2√2 −√3)(√24+3+√16 +√6)) / √12+2√2...

polinaokuneva0oumyci 01.07.2019 22:02

Вычислить значение 10ˣ при х = lg12+(log₄10)⁻¹...

Школьник5432467 01.07.2019 21:59

Найти область определения функции z=x^2+y^2...

vaynasmirnov021 02.07.2019 00:10

Раскрой скобки и подобные слагаемые . 3(х+-х)-х-4 ; х+4-5(2-+1)х-5 ; 4(х+4)-4(3-х)-х-5; х+2-4(5-+1)х-2; 2(х+-+2)х-2; если перед скобкой нет знака значит там стоит...

an02092004 01.07.2019 21:46

Найти наибольшее значение функции x³+3x²-9x-27...

данаасус 02.07.2019 00:10

Разложить на множители 3а вквадрате - 6а +3...

Популярные вопросы