Составьте квадратные уравнения, корни которого равны
Другие вопросы по теме Алгебра
Популярные вопросы
- Не купит человек ума на базаре. Определите склонение имён существительных...
3 - просклонять горы степи просторы...
1 - Построить D7 с обращениями и разрешением в F-dur...
3 - 2.Определите, какой член предложения обособлен: Несмотря на морковный румянец,...
1 - 1-тапсырма Қазақ тілі оқулығыңның 50-бетінде берілген Достық дәнегі атты...
2 - Х Тема произведения В.А. Жуковского«Сказка о царе Берендее»Выбери только...
2 - Точка P расположена внутри прямоугольника ABCD так, что PA = 5 см, PB =...
2 - Посударство 1.4. На севере граница между Караханидским государством и Кыпчакским...
2 - Read the sentence and choose the correct form. The news programmer by millions...
1 - Рузгрупируйте слова по трём столбикам: male(мужской), female(женский), both(мужской...
2
Пусть это корни уравнения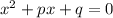
По теореме Виета:
Получили уравнение:
Домножим на 24: