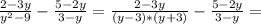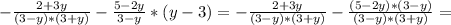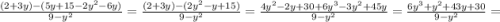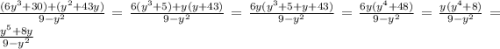СОЧ НУЖНО СЕЙЧАС СДАТЬ Выполните сложение и вычитание алгебраических дробей.
Другие вопросы по теме Алгебра
Популярные вопросы
- Скрутого берега открывается вид на волгу и на окрестные деревни....
3 - надо составить план по проекту моё хобби - моя жизнь . увлечение...
2 - Произнесите данные ниже слова. расставте в них ударение: повторит,повторить,положите,принял,приняла,облегчу,облегчишь,занял,заняли,задал...
2 - Изучите примеры. какие длинные формы есть, не имеют и не имеют?...
3 - Биринши комекшиге7/1 болигиноошеп ьерди,екиншиге6/1 болиги тиди.ушиншиге...
1 - Постройте функцию y= |log1/2 (x-2)| 10 . буду )...
2 - Что значит дёргать писю ? cкажите...
3 - Задать 5 типов вопросов (общий, специальный, к подлежащему, разделительный...
3 - 45 689 + 392 816500 001-13 295236 800 -4987989358: 28191653223215...
3 - Надо перевести на казахский язык...
1
1.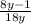
2.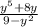
Объяснение:
1.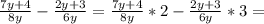
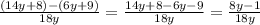
2.