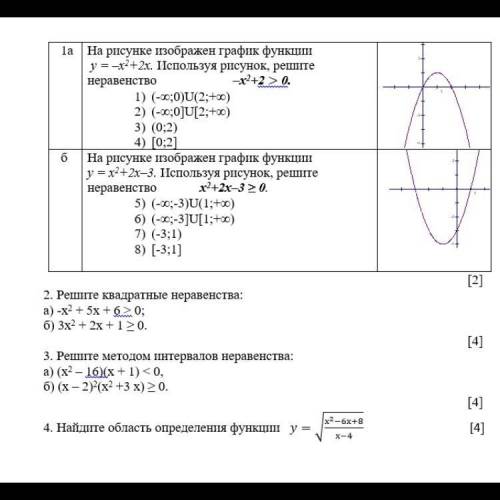
со всеми заданиями На рисунке изображен график функции у=-х^2+2х Используя рисунок решите неравенство

Чтобы решить неравенство, мы должны понять, в каких интервалах график функции ниже или выше оси x.

На рисунке видно, что график функции является параболой. Парабола направлена вниз, поскольку коэффициент при x^2 отрицателен (-1).

Мы хотим найти значения x, при которых у отрицательно. Зная, что у = -x^2 + 2x, мы можем записать неравенство:

-х^2 + 2x < 0

Теперь нам нужно определить, в каких интервалах это неравенство истинно. Для этого разложим неравенство на два уравнения:

1) -х^2 + 2x = 0
2) -х^2 + 2x > 0

Для первого уравнения, ищем значения х, при которых график функции пересекает ось x. Для этого нужно поставить выражение равным нулю и решить уравнение:

-х^2 + 2x = 0

Факторизуем это уравнение:

x(-x + 2) = 0

Таким образом, у нас две возможные точки пересечения с осью x: x = 0 и x = 2.

Теперь мы можем построить таблицу интервалов:

Интервал | -х^2 + 2x < 0 | -х^2 + 2x > 0
------------------------------------------------------
(-∞, 0) | + | -
(0, 2) | - | +
(2, +∞) | + | -

В таблице плюс (+) означает, что неравенство является истинным, а минус (-) означает, что неравенство ложно.

Таким образом, можно сделать вывод, что неравенство -х^2 + 2x < 0 верно на интервале (0, 2); а неравенство -х^2 + 2x > 0 верно на интервалах (-∞, 0) и (2, +∞).

Ученику может быть полезно также объяснить, что неравенство -х^2 + 2x < 0 означает, что значение функции у отрицательно на интервале (0, 2), а неравенство -х^2 + 2x > 0 означает, что значение функции у положительно на интервалах (-∞, 0) и (2, +∞).