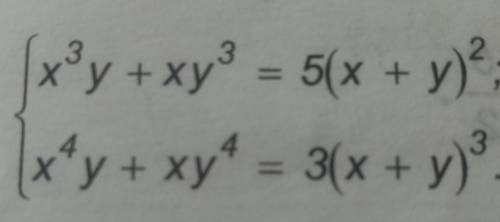
Алгебра: Сложная ситуация, что делать?

Сложная ситуация, что делать?

Ответы

hdjdhd1 07.09.2021 13:04

(0;0), (3·√2; 3/√2); (-3·√2; -3/√2); (3/√2;3·√2); (-3/√2;-3·√2)

Объяснение:

x⁴y+xy⁴=3(x+y)³

xy(x³+y³)=3(x+y)³

xy(x+y)(x²-xy+y²)=3(x+y)³

1) x+y=0⇒y=-x

x³y+xy³=5(x+y)²

x³(-x)+x(-x)³=0

-2x⁴=0

x=y=0

2) x+y≠0, x≠0, y≠0

xy(x+y)(x²-xy+y²)=3(x+y)³

xy(x²-xy+y²)=3(x+y)²

(x²-xy+y²)/3=(x+y)²/(xy)

x³y+xy³=5(x+y)²

xy(x²+y²)=5(x+y)²

(x²+y²)/5=(x+y)²/(xy)

(x²-xy+y²)/3=(x²+y²)/5

5(x²-xy+y²)=3(x²+y²)

2x²-5xy+2y²=0

2x²-4xy-xy+2y²=0

2x(x-2y)-y(x-2y)=0

(x-2y)(2x-y)=0

a) x-2y=0

x=2y

x³y+xy³=5(x+y)²

(2y)³y+2yy³=5(2y+y)²

8y⁴+2y⁴=45y²

10y⁴-45y²=0

2y⁴-9y²=0

y²(2y²-9)=0

2y²-9=0

2y²=9

y²=9/2

y=±3/√2

x=2y=2·(±3)/√2=±3·√2

b) 2x-y=0

y=2x

Аналогично а)

x=±3/√2

y=2y=2·(±3)/√2=±3·√2

ПОКАЗАТЬ ОТВЕТЫ

акылбек5 07.09.2021 13:04

$(0 \ ; \ 0) \ ; \ \bigg (3\sqrt{2} \ ; \ \dfrac{3\sqrt{2}}{2} \bigg ) \ ; \ \bigg (-3\sqrt{2} \ ; \ -\dfrac{3\sqrt{2}}{2} \bigg ) \ ; \ \bigg (\dfrac{3\sqrt{2}}{2} \ ; \ 3\sqrt{2} \bigg ) \ ; \ \bigg (-\dfrac{3\sqrt{2}}{2} \ ; \ -3\sqrt{2} \bigg ) \ ;$

Объяснение:

$D(x,y): \ x \neq -y \ ;$

$\displaystyle \left \{ {{x^{3}y+xy^{3}=5(x+y)^{2}} \atop {x^{4}y+xy^{4}=3(x+y)^{3}}} \right. \Leftrightarrow \left \{ {{xy(x^{2}+y^{2})=5(x+y)^{2}} \atop {xy(x^{3}+y^{3})=3(x+y)^{3}}} \right. ;$

Разделим верхнее уравнение на нижнее:

$\dfrac{xy(x^{2}+y^{2})}{xy(x^{3}+y^{3})}=\dfrac{5(x+y)^{2}}{3(x+y)^{3}} \ ;$

$\dfrac{x^{2}+y^{2}}{x^{3}+y^{3}}=\dfrac{5}{3(x+y)} \ ;$

$\dfrac{x^{2}+y^{2}}{(x+y)(x^{2}-xy+y^{2})}=\dfrac{5}{3(x+y)} \quad \bigg | \quad \cdot (x+y)$

$\dfrac{x^{2}+y^{2}}{x^{2}-xy+y^{2}}=\dfrac{5}{3};$

$\dfrac{x^{2}-xy+y^{2}}{x^{2}+y^{2}}=\dfrac{3}{5} \ ;$

$\dfrac{x^{2}+y^{2}}{x^{2}+y^{2}}-\dfrac{xy}{x^{2}+y^{2}}=\dfrac{3}{5} \ ;$

$1-\dfrac{xy}{x^{2}+y^{2}}=\dfrac{3}{5} \ ;$

$\dfrac{xy}{x^{2}+y^{2}}=1-\dfrac{3}{5} \ ;$

$\dfrac{xy}{x^{2}+y^{2}}=\dfrac{2}{5} \ ;$

$\dfrac{x^{2}+y^{2}}{xy}=\dfrac{5}{2} \ ;$

$\dfrac{x^{2}}{xy}+\dfrac{y^{2}}{xy}=\dfrac{5}{2} \ ;$

$\dfrac{x}{y}+\dfrac{y}{x}=\dfrac{5}{2} \ ;$

Введём замену:

$t=\dfrac{x}{y} \Rightarrow \dfrac{y}{x}=\dfrac{1}{t} \ ;$

Перепишем уравнение с учётом замены:

$t+\dfrac{1}{t}=\dfrac{5}{2} \quad \bigg | \quad \cdot 2t$

$2t^{2}+2=5t;$

$2t^{2}-5t+2=0;$

$D=b^{2}-4ac \Rightarrow D=(-5)^{2}-4 \cdot 2 \cdot 2=25-16=9;$

$t_{1}=\dfrac{-b+\sqrt{D}}{2a} \Rightarrow t_{1}=\dfrac{-(-5)+\sqrt{9}}{2 \cdot 2}=\dfrac{5+3}{4}=\dfrac{8}{4}=2;$

$t_{2}=\dfrac{-b-\sqrt{D}}{2a} \Rightarrow t_{2}=\dfrac{-(-5)-\sqrt{9}}{2 \cdot 2}=\dfrac{5-3}{4}=\dfrac{2}{4}=\dfrac{1}{2};$

Вернёмся к замене:

$\dfrac{x}{y}=2 \quad \vee \quad \dfrac{x}{y}=\dfrac{1}{2} \ ;$

$x=2y \quad \vee \quad x=\dfrac{y}{2} \ ;$

Вернёмся к системе:

$\displaystyle \left \{ {{x=2y} \atop {(2y)^{4} \cdot y+2y \cdot y^{4}=3(2y+y)^{3}}} \right. \vee \left \{ {{x=\dfrac{y}{2}} \atop {\bigg (\dfrac{y}{2} \bigg )^{4} \cdot y+\dfrac{y}{2} \cdot y^{4}=3 \bigg (\dfrac{y}{2}+y \bigg )^{3}}} \right. \Leftrightarrow$

$\displaystyle \Leftrightarrow \left \{ {{x=2y} \atop {16y^{5}+2y^{5}=3 \cdot 27y^{3}}} \right. \vee \left \{ {{x=\dfrac{y}{2}} \atop {\dfrac{y^{5}}{16}+\dfrac{y^{5}}{2}=3 \cdot \dfrac{27y^{3}}{8}}} \right. \Leftrightarrow \left \{ {{x=2y} \atop {18y^{5}-81y^{3}=0}} \right. \vee$

$\displaystyle \vee \left \{ {{x=\dfrac{y}{2}} \atop {y^{5}+8y^{5}=3 \cdot 27y^{3} \cdot 2}} \right. \Leftrightarrow \left \{ {{x=2y} \atop {2y^{5}-9y^{3}=0}} \right. \vee \left \{ {{x=\dfrac{y}{2}} \atop {9y^{5}-6 \cdot 27y^{3}=0}} \right. \Leftrightarrow$

$\displaystyle \Leftrightarrow \left \{ {{x=2y} \atop {y^{3}(2y^{2}-9)=0}} \right. \vee \left \{ {{x=\dfrac{y}{2}} \atop {y^{5}-18y^{3}=0}} \right. \Leftrightarrow \left \{ {{x=2y} \atop {y^{3}=0}} \right. \vee \left \{ {{x=2y} \atop {2y^{2}-9=0}} \right. \vee$

$\displaystyle \vee \left \{ {{x=\dfrac{y}{2}} \atop {y^{3}(y^{2}-18)=0}} \right. \Leftrightarrow \left \{ {{x=0} \atop {y=0}} \right. \vee \left \{ {{x=2y} \atop {y^{2}=\dfrac{9}{2}}} \right. \vee \left \{ {{x=\dfrac{y}{2}} \atop {y^{3}=0}} \right. \vee \left \{ {{x=\dfrac{y}{2}} \atop {y^{2}-18=0}} \right. \Leftrightarrow$

$\displaystyle \Leftrightarrow \left \{ {{x=0} \atop {y=0}} \right. \vee \left \{ {{x=2y} \atop {y=\pm \sqrt{\dfrac{9}{2}}}} \right. \vee \left \{ {{x=0} \atop {y=0}} \right. \vee \left \{ {{x=\dfrac{y}{2}} \atop {y=\pm \sqrt{18}}} \right. \Leftrightarrow \left \{ {{x=0} \atop {y=0}} \right. \vee \left \{ {{x=2y} \atop {y=\pm \dfrac{3}{\sqrt{2}}}} \right. \vee$

$\displaystyle \vee \left \{ {{x=\dfrac{y}{2}} \atop {y=\pm 3\sqrt{2}}} \right. \Leftrightarrow \left \{ {{x=0} \atop {y=0}} \right. \vee \left \{ {{x=2y} \atop {y=\pm \dfrac{3\sqrt{2}}{2}}} \right. \vee \left \{ {{x=\pm \dfrac{3\sqrt{2}}{2}} \atop {y=\pm 3\sqrt{2}}} \right. \Leftrightarrow \left \{ {{x=0} \atop {y=0}} \right. \vee$

$\displaystyle \vee \left \{ {{x=\pm 3\sqrt{2}} \atop {y=\pm \dfrac{3\sqrt{2}}{2}}} \right. \vee \left \{ {{x=\pm \dfrac{3\sqrt{2}}{2}} \atop {y=\pm 3\sqrt{2}}} \right. \ ;$