Алгебра: Скоротіть дріб 27a³b²/18ab⁸

Скоротіть дріб 27a³b²/18ab⁸

Ответы

varkraft 19.09.2021 06:20

ответ в файле

Объяснение:

при делении чисел со степениями - степени вычитаются

ПОКАЗАТЬ ОТВЕТЫ

baybiboom 19.09.2021 06:20

$\frac{27*a^3*b^2}{18*a*b^8}=1,5*a^2*\frac{1}{b^6}=\frac{3}{2}*a^2*\frac{1}{b^6}=\frac{3*a^2*1}{2*1*b^6}=\frac{3*a^2}{2*b^6}$

Объяснение:

Степень числа, это произведение множителей, каждый из которых величиной , 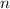раз подряд, где

a^n=a*a*a*a*a*...*a

Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого числа вычитают показатель степени делителя:

$\frac{a^m}{a^n}=a^{m-n$

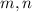Где m,n - любые натуральные числа, с условием, что .

Запишем наш пример:

$\frac{27*a^3*b^2}{18*a*b^8}$

Для наглядности решения данный пример можно разделить на три части, и согласно свойству частного степеней, которое я записал выше можно было проще решить данный пример.

Первой частью будут известные числа:

$\frac{27}{18}=\frac{3^3}{3^2*2}=\frac{3^{3-2}}{2}=\frac{3^1}{2}=\frac{3}{2}=1,5\\27=3*3*3=3^3;\\18=3*3*2=3^2*2$ (1)

Теперь запишем отдельно деление переменной :

$\frac{a^3}{a^1}=a^{3-1}=a^2$ (2)

Далее запишем переменную :

$\frac{b^2}{b^8}=b^{2-8}=b^{-6}=\frac{1}{b^6}$ (3)

Так как по определению отрицательной степени: $b^{-n}=\frac{1}{b^n}$

Теперь совместим (1), (2) и (3):

$1,5*a^2*\frac{1}{b^6}=\frac{3}{2}*a^2*\frac{1}{b^6}=\frac{3*a^2*1}{2*1*b^6}=\frac{3*a^2}{2*b^6}$ - в дальнейшем данную дробь сократить невозможно, это и будет ответ.