Скорость одного поезда на 10 км/ч больше, чем скорость другого, и поэтому путь в 80 км он проходит на 16 мину быстрее. найдите скорость каждого поезда.
Другие вопросы по теме Алгебра
Популярные вопросы
- Суретти колданып коректик тизбек жане коректик тор курастырыныз 7 сынып...
2 - Вставьте пропущенные слова, используя словарик. Зрительная трубка (тубус) — основная...
1 - Какую делают нашу речь пословицы и поговорки?...
3 - Роботтардың адам өміріне әсері эссе ...
2 - Задание на закрепление «Истина/Ложь» 1. В раннем палеолите со стороны Индийского...
2 - я тоже вам отвечу на ваши вопросы...
1 - Первое число в 7 раз больше второго, а их сумма равна 40. Найди первое число....
2 - Тургеш каганатындпгы алгашкы каган ...
2 - Выполните действия: 1) 38 : 17 - 4 832 : 16;2) 3 596 — 3 596 : (2 314 - 2 256)РЕШИТЕ...
2 - (48-6):7+72:8:3=(8•4-6•2):5•(4:2)=...
1
ответ: 50 км/ч и 60 км/ч
Пусть скорость первого поезда равна x км/ч.
Тогда скорость второго равна x + 10 км/ч.
Время первого поезда -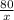 часов.
часов.
Тогда время второго -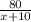 .
.
Но также мы знаем, что время второго поезда меньше на 16 минут, то есть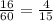 часа. Можно составить уравнение и решить его:
часа. Можно составить уравнение и решить его:
Очевидно, что первый корень (-60) не подходит, так что скорость первого поезда равна 50 км/ч, а второго - 50 + 10 = 60 км/ч.
Ура! Задача решена! Удачи!