Сколько корней заданного уравнения принадлежит указанному промежутку: 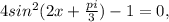 x∈[0;3].
x∈[0;3].
Другие вопросы по теме Алгебра
Популярные вопросы
- Очень вычислите значения переменных A) x:=10; y:=2 + x mod 3; c:=15 mod...
3 - Продемонстрируйте ваши знания итогов и последстви голинского договора...
3 - 2-тапсырма. «Қан мен тер» романынан берілген үш үзіндіге ат қой. Оны...
1 - Подчеркните однородные члены и составьте схемы предложений с однородными...
1 - Пропан-пропан-2 хлорпропан-пропанол 2-изопропилат кальция...
2 - Выпиши предложение с обособленным предложением...
2 - Для вещества гексан CH3-CH2-CH2-CH2-CH2-CH3 составьте структурные формулы...
2 - Упражнение 3 Прочтите следующий текст и вставьте логические связки, где...
1 - Выполните задания по английскому языку...
2 - определить массу Солнца, если известно, что сила тяготения между Землей...
1
Давайте начнем пошагово:
1. Запишем заданное уравнение: 4sin^{2}(2x+\frac{\pi}{3})-1=0.
2. Раскроем квадрат синуса, используя формулу: sin^{2}\theta = \frac{1 - \cos(2\theta)}{2}. Получим: 4(\frac{1 - \cos(4x+\frac{2\pi}{3})}{2})-1=0.
3. Упростим уравнение: 2(1 - \cos(4x+\frac{2\pi}{3}))-1=0.
4. Раскроем скобки и упростим дальше: 2 - 2\cos(4x+\frac{2\pi}{3})-1=0.
5. Сгруппируем константы: 1 - 2\cos(4x+\frac{2\pi}{3})=0.
6. Перенесем единицу на другую сторону: 2\cos(4x+\frac{2\pi}{3}) = 1.
7. Разделим уравнение на 2: \cos(4x+\frac{2\pi}{3}) = \frac{1}{2}.
8. Решим уравнение для \cos\theta = \frac{1}{2}. Найдем значения \theta, при которых \cos \theta равно \frac{1}{2}. Обычно это значения углов, находящихся в первом и четвертом квадрантах. В данном случае это будут значения \frac{\pi}{3} и \frac{5\pi}{3}.
9. Запишем уравнение для первого значения: 4x+\frac{2\pi}{3} = \frac{\pi}{3}. Решим его, чтобы найти значение x: 4x = \frac{\pi}{3} - \frac{2\pi}{3}. Таким образом, получаем x = -\frac{\pi}{6}.
10. Запишем уравнение для второго значения: 4x+\frac{2\pi}{3} = \frac{5\pi}{3}. Решим его, чтобы найти значение x: 4x = \frac{5\pi}{3} - \frac{2\pi}{3}. Таким образом, получаем x = \frac{\pi}{2}.
11. Теперь проверим, принадлежат ли найденные значения x указанному промежутку [0;3]. Очевидно, что -\frac{\pi}{6} не принадлежит этому промежутку, так как это отрицательное значение. Но \frac{\pi}{2}, которое мы получили вторым решением, входит в указанный промежуток.
Таким образом, ответ на вопрос будет: заданное уравнение имеет 1 корень, принадлежащий промежутку [0;3]. Этим корнем является x = \frac{\pi}{2}.