Сколько корней имеет уравнение:√1999-2000 х + √2001x-2000=1?
Другие вопросы по теме Алгебра
Популярные вопросы
- Автонавантажувач рухається рівномірно вздовж ряду контейнерів. Контейнери,...
3 - 6. Какое утверждение верно? А. Ветер всегда дует в том направлении,...
2 - Какая отрасль химической промышленности преобладает в России?...
2 - Turn from Active into Passive. 1. People often use this common phrase...
2 - Разделите слова на две группы. Исконно русские слова Заимствованные...
3 - В чем причины экономического подъема Голландии в 17 веке?...
2 - Щоб забезпечити вихід татарам із котловини, Тугар Вовк має намір...
2 - Всі хто знають сольфеджіо до ть будь ласка в....
1 - 1)складіть передумови Берестейської унії желательно полный, раскрытый...
1 - Для плавления металла массой 0,6 кг затратили 50,4 кДж тепла. Используя...
1
Объяснение:
В задании немного некорректно написаны корни, поэтому:
Если задание такое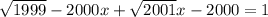 , то
, то
перегрупировав слагаемые мы получили линейную функцию, которой максимум 1 корень. Так как в эта функция зависит от х, то 1 решение гарантированно.
Если задание такое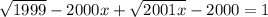 , то
, то
Возводив в квадрат мы получим квадратное уравнение, у которого максимум 2 корня. но поскольку везде будут знаки + (мы возведём в квадрат, чтобы избавится от корня), и свободный член не равен 0, то решений нет, так как дискриминант меньше нуля.