Сколько действительных корней имеет уравнение logx(3x^2-2)=4
Другие вопросы по теме Алгебра
Популярные вопросы
- Территориальный раздел казацкой Украины на Левобережную и Правобережную был...
3 - НУЖНА ЗАРАНЕЕ Знайти значення кореня...
1 - Дати назви запропонованим ізомерам: А) СН 2 = СН – СН 2 – СН 3 Б) СН 3 – СН...
2 - Что необходимо отметить в оценочной части рецензии?...
1 - Составить сложные предложения с несколькими придаточными...
2 - Постройте график функций y=2x+3 С графика найдите: а)y(-3); б)у,если х=4;...
3 - Розташування кінцівок відносно тулуба птахів...
3 - 13.1. Парашутист опускається, рухаючись рівномірно пря- молінійно. Дії яких...
2 - Опредлите имя китайского историка, который описывал историю Уйсунов в своих...
2 - Производительность труда рабочего в течение дня задаётся формулой f(t) = 0,00625t4...
3
Для начала найдем ОДЗ:
Первое уравнение решим отдельно.
3x^2 -2>0
3x^2 -2=0
x^2=2/3
Чертим координатную прямую, отмечаем точки, расставляем знаки. Рисунок добавлю во влажения.
Решением этого уравнения будет промежуток
А решением системы будет являться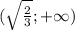
Теперь начнем решение. Представим 4 в виде логорифма по основанию x.
Так как основания равны, то знак логорифма можно опустить.
3x^2 -2 =x^4
x^4 - 3x^2 +2 =0
Это биквадратное уравнение. Введем обозначения
x^2 = a,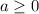
a^2 -3a+2=0
По теореме Виета a1=2, a2=1
Теперь найдем х:
x^2= 2 x^2=1
Выберем корни, входящие в ОДЗ. Таковыми являются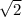 и 1.
и 1.
ответ: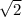 и 1
и 1
logx(3x^2-2)=4
3x^2-2=x^4
-x^4+3x^2-2=0 (-1)
x^4-3x^2+2=0
пусть x^2=t
t^2-3t+2=0
D = ( 9 / 4 ) - ( 1 * 2 ) = 1.
D>0
1) t1 = ( 3 )+v(1) / 2 = 2
2) t2 = ( 3 )-v(1) 2 = 1
замена x^2=2 x^2=1
x=корен2 x=1