Скажите как называются функции графиков и укажите их возраствния и убывания.

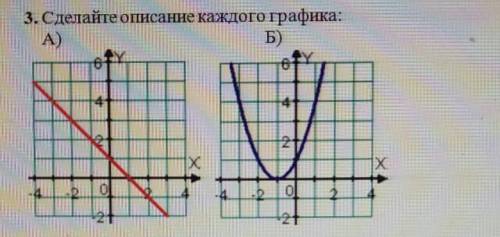
а - ленейная б - квадратная

Объяснение:

Если k>0, то линейная функция y=kx+b возрастает. если k<0, то линейная функция y=kx+b

Если ветви направлены вверх, то квадратичная функция сначала убывает от –∞ до самой вершины параболы, а затем начинает возрастать от вершины до +∞.

Объяснение: А) Прямая-график линейной функции у=kx+b, k<0, т.к. угол, образованный прямой с положительным направлением оси ОХ-тупой; поэтому функция убывающая на (-∞; +∞);  т.к. график проходит через точки (0;1) и (1;0), то функция задана формулой у= -х +1.       Б)Парабола-график квадратичной функции у=ах²+bx+c; так как вершина параболы в точке (-1;0) и она касается оси ОХ,а  ветви направлены вверх, значит а>0: можно задать формулой у =(х+1)². Функция убывает на (-∞;-1} и возрастает на [-1; +∞).