Система уравнений
|x|+|y|=4
x^2+y^2=a
имеет четыре решения, если параметр a
Другие вопросы по теме Алгебра
Популярные вопросы
- решите уравнение x^2-3x-4 = 3^3x * (1 - 3^(x^2 -3x - 4))...
3 - 1)соедините последовательно точки A,B и С Определите вид полученного треугольника...
1 - Водяний насос за 10 хвилин піднімає 500 літрів води на висоту 30 м. Яка...
3 - Д7,Д65,Д43,Д2 с обращением от звука Си (не тональность а звук) ...
2 - Знайдіть масу кожного вантажу, якщо маса двох важків становить 30 кг....
3 - Поясни значення слив Гайда, негайно, марити...
3 - Два круга касаются друг друга. Радиус большого круга 26 см, а малого круга...
2 - До іть будь ласка с шостим завданням...
3 - нужно тут словообразование...
1 - Опишите любые 2 вида (1-растение, 1- животное) по плану: 1. Место вида...
2
16
Объяснение:
|x| + |y| = 4 - квадрат с вершинами в точках (0;4), (4;0), (0;-4), (-4;0)
x = 0 => y = 4, y = -4
y = 0 => x = 4, x = -4
x² + y² = a - окружность радиуса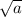
x = 0 => y =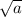 , y = -
, y = -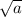
y = 0 => x =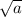 , x = -
, x = -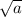
Система будет иметь 4 решения, когда окружность и квадрат будут пересекаться в 4х точках =>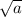 = 4 => a = 4² = 16
= 4 => a = 4² = 16