Sin2=3/5 α-I четв.
cos2-? tgα-? ctgα-?
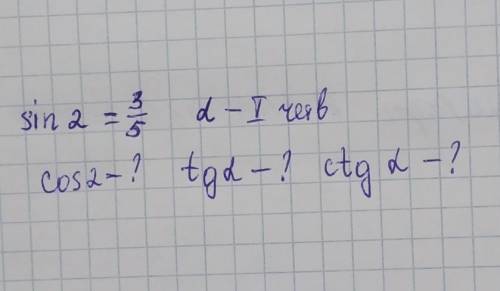
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие предложения является правильными? а)молодая деректор васильева...
1 - Und was machen sie? ergänzt.1.der .der .der gä.der...
2 - Все части речи в языке с правилами, и предложения к каждой части...
2 - Масштаб на карте равен 1: 1000000. определите расстояние на местности,...
3 - А^10/(а^4)^2*(а^3/а^2) завтра аттестационная нужно решить не получается...
3 - Написать сичинение о том как выполняете любимую и необходимую работу....
1 - Изменить предложения используя страдательный залог: 1. you will...
3 - А)в прямоугольнике абсd ab=24см, ас=25см. найдите площадь прямоугольника....
1 - Вниже предложении найдите несогласованное определение и определяемое...
1 - Какая прямая является касательной к окружности с центром в точке...
2
cosα = 4/5;
tgα = 3/4;
ctgα = 1 1/3.
Объяснение:
1) sin²α+ cos²α= 1
cos²α = 1 - sin²α = 1 - (3/5)² = 25/25 - 9/25 = 16/25;
Так как α - угол I четверти, то сosα > 0, тогда
сosα = +√(16/25) = 4/5.
2) tgα = sinα/cosα = 3/5 : 4/5 = 3/5 • 5/4 = 3/4.
3) tgα • ctgα = 1, тогда
ctgα = 1/tgα = 1 : 3/4 = 4/3 = 1 1/3.