Sin120=sin(90+30)=+sin30
cos120=cos(180-60)=-cos60
откуда взялись числа, которые в скобках? объясните подробно

Ответы

dims12 01.09.2020 10:24

Смотри, cos120 нету (в таблице), а найти его значение нужно, то мы используем круг и его четверти. Смотреть картинки. Весь круг это 360 градусов, тоесть если нам нужно найти sin390 мы это расписываем sin390=sin(360+30)=sin30 360 градусов это круг, мы возвращаемся к исходу: 0 градусов. Значит тот остаток в виде 30 градусов мы и считаем его.

Также от этого зависимы и значение + и - (Смотреть картинки). Мы ищем sin120, во второй чверти его значение + , значит sin того градуса который мы получили будет иметь знак +

Чверти считают от начала отсчета (от 0 градусов)

В правой части равенства ставят этот знак имеющий левая часть выражения при условии, что альфа острый угол.

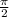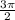Если в левой части выражения \ формулы аргумент выглядит $\frac{\pi }{2}$ ± α ; $\frac{3\pi }{2}$ ± α , то функция sin меняется на cos; ctg на tg; и наоборот; а если аргмент выглядит π ± α; 2π ± α функция не меняется.