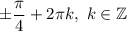|sin(x)|=cos(x)
Решить уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Редактор отредактировал статью и ее объем уменьшился на 2 страницы. каждая страница...
1 - До обеда мастер изготовил 21 деталь, что составляет 70% всего заказа. сколько...
3 - Найдите количество трёхзначных чисел , которые делятся на 3 но не делятся на...
3 - Напишите одно слово 1. королевская резиденция при людвике 14 слово состоит из...
1 - Смесь газов состоит из водяного пара и окиси углерода. массовая доля вод. пара...
3 - Вмагазине было 86 ковров.когда купили 46 больших и несколько маленьких ковров,то...
1 - Сравните жизнь и быт кочевников и оседлых земледельцев.сделайте выводы....
3 - Измените глаголы в страдательном залоге в активный.(change verbs in passive...
3 - Занятые какая часть речи глагол или прилагательное...
2 - 2. дан треугольник abc со сторонами ab=10 bc=14 ac=15 , . найти: а) площадь;...
3
Раскроем модуль:
ответ: