Sin 2x = - cos 2 x решите уравнение (подробное решение)
Другие вопросы по теме Алгебра
Популярные вопросы
- Установіть відповідність між формулою речовини та загальною кількістю...
3 - 1. Расположите в порядке усложнения варианты покровов тела. А) Кутикула...
1 - 1. Реакцией нейтрализации называется реакция между: А) Кислотой и...
3 - Үстеулердің түрлерін ажыратып, әр үстеуге етістіктерді тіркестіріп...
3 - В первом элеваторе было зерна в 3 раза больше, чем во втором. Из первого...
2 - 256. Определите, какая часть фигуры закрашена. Попробуйте выра- зить...
3 - Дати письмову відповідь на питання ,, Чому Шекспір назвав трагедію,,ДЖУЛЬЄТТА...
3 - Запишіть речення, зробіть синтаксичний розбір. Розберіть дієприслівник...
1 - Алюміній+сірка=натрій+кисень=...
2 - Где в спб есть греческие боги?...
1
(см. объяснение)
Объяснение:
Уравнение решено!
Замечу, что можно было поделить все на cos2x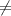 0 и решать через tg.
0 и решать через tg.