Шукаю геніїв математики, буду вдячний​

Объяснение:

Производная всюду непрерывна.

Находим производную функции:

Находим действительные корни производной:

Имеем одну критическую точку х₀=2.

Исследуем эту точку:

при х₀<2  y'>0,

при х₀>2  y'>0       ⇒

По первому достаточному признаку существования экстремума функции следует, что в данной точке х₀=2 экстремума нет.   ⇒

Функция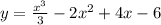 не имеет точек экстремума.