Сформулируйте решение системы неравенств
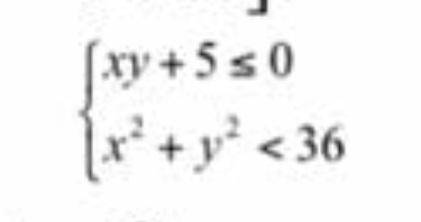
Другие вопросы по теме Алгебра
Популярные вопросы
- Составь небольшое сочинение на тему *культура моего народа если что...
3 - Предложения: boris (to take) a shower now. the girls (to go) for...
1 - Напишите сочинение на тему культура речевого общения(без сочинений...
1 - Два положительных заряда 0,2 и 1,8 мккл закреплены на расстоянии...
1 - Девочка каждый день читала одинаковое число страниц. первую книгу...
1 - Сочинения на с переводом по теме что я знаю и умею...
3 - За 34 плз в ходе теннисного турнира, в котором принимали участие...
1 - Синформатикой, не понимаю её вообще( 1.что не может сравнивать простое...
3 - Какой объем углекислого газа образуется при разложении карбоната...
1 - Какое свойство организмов служит источником искусственного и естественного...
2
В данном случае, у нас есть два неравенства:
1) 2x ≤ 10
2) 3y + 4 < 16
Давайте начнем с первого неравенства: 2x ≤ 10. Чтобы найти решение этого неравенства, мы должны выразить x. Для этого нужно разделить обе части неравенства на 2 (поскольку 2 - это коэффициент переменной x):
2x/2 ≤ 10/2
x ≤ 5
Теперь, перейдем ко второму неравенству: 3y + 4 < 16. Чтобы найти решение этого неравенства, мы должны выразить y. Для этого нужно вычесть 4 из обеих частей неравенства:
3y + 4 - 4 < 16 - 4
3y < 12
Затем, делим обе части неравенства на 3 (поскольку 3 - это коэффициент переменной y):
(3y)/3 < 12/3
y < 4
Итак, мы получили два неравенства:
1) x ≤ 5
2) y < 4
Окончательное решение системы неравенств будет заключаться в том, чтобы найти значения переменных x и y, которые удовлетворяют обоим неравенствам одновременно. В данном случае, решением будет:
x ≤ 5 и y < 4
Это значит, что значения переменной x должны быть меньше или равны 5, а значения переменной y должны быть меньше 4. Например, если x равно 3 и y равно 2, то оба неравенства будут истинными. Однако, если x равно 6 и y равно 5, то первое неравенство будет ложным.
Надеюсь, я понятно объяснил решение системы неравенств и помог тебе понять это математическое понятие! Если у тебя возникнут еще вопросы, не стесняйся спрашивать. Я всегда готов помочь!