Сэтим , нужно определить сколько ответов имеют уравнения или неравенства.
Другие вопросы по теме Алгебра
Популярные вопросы
- Задача на дробь. 3-им примером нам учитель задал, но не успел объяснить как...
1 - По реформе 1867-1868 гг. области делились на...
3 - Какие инструменты применяют при фрезировании...
2 - Красворд на 10 слов Тема: олимпийские игры в древности (5 класс) Нужно...
2 - Уекел 1. В 1237 г. поход на Русь предпринял:Tа) Чингисхан б) Батый в) Тохтамыш...
3 - Речення: Сонцю над світом горіти., Є а)означено-особове, б)неозначено-особове...
2 - Преобразуйте в многочлен:1)(a+7)^2 2)(2x-y)^2...
1 - В результате межконфессионального конфликта государство S распалось. Этот пример...
2 - 8. Кількість атомів в молекулі Bas(PO4)2 становить:а) 8;б) 3;в) 11: г) 13...
3 - V MUO2/1Получить – при кусков....
1
Первое задание
Сделаем замену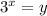 , при этом
, при этом 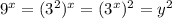 . Получим уравнение:
. Получим уравнение:
Тут по теореме Виета сразу видно, что первый корень равен единице. Тогда второй корень равен –9.
Вернёмся к исходной переменной:
ответ: одно решение.
Второе задание
Основания степеней больше единицы, поэтому, переходя к неравенству показателйе, знак сохранится:
Приравняем левую часть выражения к нулю, решим через дискриминант и разложим на множители:
Применив метод интервалов, получим, что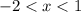 . Поскольку неравенство строгое, имеем два целых решения: –1 и 0.
. Поскольку неравенство строгое, имеем два целых решения: –1 и 0.
ответ: два решения.
Третье задание
ОДЗ:
Или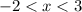
Или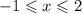 (ведь речь о целых числах).
(ведь речь о целых числах).
Теперь решим уравнение:
Решений было бы бесконечное количество, если бы не ОДЗ: под него подпадают только числа –1, 0, 1, 2 (то есть четыре штуки).
ответ: четыре решения.
Четвёртое задание
ОДЗ:
Основание логарифма больше единицы, поэтому при переходе к неравенству выражений под логарифмом знак сохранится:
Решений было бы бесконечное количество, но с учётом ОДЗ получим: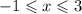 . Здесь решениями будут числа –1, 0, 1, 2, 3.
. Здесь решениями будут числа –1, 0, 1, 2, 3.
ответ: пять решений.