Сделайте только номер 15 2-ой и 4-ый доказать что прогрессия является бесконечно убывающей 2)1 3 в дроби ( одна третья ) , 1 9 ( одна девятая ) , 1 27 ( одна двадцать седьмая ) ; 4) -64 , -32 , -16 .
Ответы
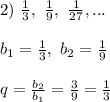
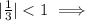 прогрессия бесконечно убывающая.
прогрессия бесконечно убывающая.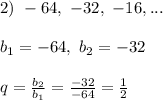
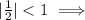 прогрессия бесконечно убывающая.
прогрессия бесконечно убывающая.
Другие вопросы по теме Алгебра
Популярные вопросы
- Площадь квадрата 16 см2. найдите чему равна площадь: 3/4 квадрата...
2 - )какое число будет следующим в ряду 6 12 36 144 720 а) 1024 б) 2140...
2 - Напишите уравнение реакций солеобразования доказывающие характер оксидов...
2 - Две стороны треугольника 6 см и 10 см, а угол между ними равен 120...
1 - Какая модель является материальной(натурной)?...
2 - Найдите расстояние от одного города до другого если на карте масштаб...
1 - Найдите облость определения игрик равно корень из 2 икс квадрат минус...
2 - Втреугольнике abc ac=bc. угол c равен 96 градусам. найдите внешний...
3 - Впиши пропущенные числа так чтобы получились верные равенства 1/3...
1 - За какое время можно передать 10 гбайт информации, при скорости 100...
1