СДЕЛАЙТЕ ПОЛНОСТЬЮ 3, 4,5 И 6 ЗАДАНИЕ. КТО НЕ ЗНАЕТ НЕ ПИШИТЕ ИНАЧЕ БАН! ​

По Виету х=4; х=-1/2;   (х-4)(х+1/2)≤0

-1/24

+                             -                 +

х∈[-1/2;4]   Целые 0; 1;2;3;4.

2. х<1/7

2(x-1)(x+1/2)≤0

___-1/21

+               -               +

пересечением множеств

(-∞;1/7)∩[-1/2;1]=[-1/2;1/7)

3. неравенство равносильно системе

х²(3-х)(х-4)²≤0

х≠4

034

+            +           -          -

x∈[-3;4)∪(4;+∞)∪{0}

4. найдем пересечение решений неравенств решением первого служит х∈(-∞;+∞), т.к. дискриминант меньше нуля. он равен 9-16=7, решением второго (х-4)*(х+4)≤0

-44

+              -           +

х∈[-4;4] есть х∈[-4;4]

Целые 0, 1, 2, 3, 4.

О.Д.З.:

Очевидно, что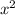 в числителе и 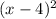в знаменателе будут положительный при любых 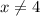. Значит решение сводится к решению неравенства 3-x ≤0

Тогда с учётом О.Д.З.

Дискриминант отрицательный, корней нет. Проверим, выполняется ли неравенство. Возьмём x = 5 (можно взять любое значение):

25-3·5+4 = 25-15+4 = 14 > 0

Первое неравенство выполняется при любых x. Значит решение второго неравенства будет решением всей системы.