Сделайте ,покозательные уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- 3. Задание Даны материалы: растительное масло, вода, стакан, средство...
1 - Окшау сөздерді жасалу жолына карай топтастырып жазындар. Тегiнде, кап,...
3 - Задание 3. Дайте характеристику причастиям по образцу: Веривший сын...
1 - Задача На сколько уменьшиться или увеличиться ставка процента, если...
2 - Тормозной путь автомобиля, который движется со скоростью 72 км/ч, равен...
1 - Казак тили 18 Бет 9тапсырма 5класс поставлю звезды...
2 - Поставьте слова в скобках в нужной форме с предлогом или без предлога....
3 - решить по чертежу ♥очень надо в течении 40 минут...
2 - В строке «И равен был неравный спор» используется особый художественный...
1 - Мини-соченение с причастиями...
2
Первое уравнение
Вынесём множитель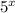 за скобки:
за скобки:
Второе уравнение
Сделаем замену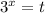 :
:
Вернёмся к исходной переменной:
а)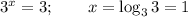
б)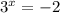
Показательная функция принимает только положительные значения, поэтому последнее уравнение не имеет решений.
ответ: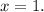
Третье уравнение
Сделаем замену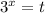 :
:
Вернёмся к исходной переменной:
а)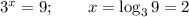
б)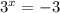
Показательная функция принимает только положительные значения, поэтому последнее уравнение не имеет решений.
ответ: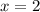 .
.